Blog of Yang
0%

scaleOIJ

Posted on Edited on In
Symbols count in article: 7.5k Reading time ≈ 14 mins.

Scalable OIJ on ModernMulticore Processors in OpenMLDB

动机

● 该研究基于OpenMLDB平台，旨在提高现代多核服务器上进行OIJ的延迟和吞吐量。

● Ooline Interval Join（OIJ）是一种常见的基于时间数据库的区间连接方法，用于在数据流中连接具有重叠时间区间的元组。然而，现有的OIJ解决方案（key-OIJ）在处理大规模数据时存在性能瓶颈，因此需要进行优化。

● 本研究通过实验分析现有解决方案的设计空间和关键问题，并提出了一种新的解决方案——Scale-OIJ，以提高OIJ的性能。本研究的重要性在于，它提供了一种有效的方法来优化OIJ，从而提高时间数据库的处理效率，为机器学习等领域的实时数据处理提供更好的支持。

● Dataset：Both real-world and synthetic

● Indicator: Throughput(mean value); Lateness(CDF); Unbalancedness(standarddeviationof workloads); LCC miss( last-level cach miss)

简单对比

● 在文本中，作者提出了一种名为Scale-OIJ的新方法，用于实现可扩展的在线区间连接。与现有的OIJ解决方案Key-OIJ相比，Scale-OIJ具有以下区别：

● Scale-OIJ：

● - 使用SWMR(Single-Writer-Multiple-Reade) Time-Travel数据结构，可以在不锁定数据的情况下进行并发读写操作。

● - 使用动态平衡调度，可以在多个线程之间动态分配工作负载，以实现更好的负载均衡。● - 使用增量窗口聚合，可以避免重复计算重叠窗口，从而提高计算效率。

● Key-OIJ：

● - 使用基于键的分区并行化策略，可以将输入元组并发地与相同键的缓冲区连接。● - 为了处理潜在的乱序流到达，元组只能在一段时间后才能被删除。

传统方法的缺点—key-OIJ

● 1. 处理无序数据的成本高昂：Key-OIJ算法在处理无序数据时表现不佳。特别是在大延迟的情况下，需要进行昂贵的无序数据操作。在Flink中，每个连接操作都需要进行完整的数据扫描，导致性能下降。

● 2. 负载不平衡：Key-OIJ算法采用基于键的分区策略，这可能导致负载不平衡的问题。特别是在键数较少的情况下，工作负载可能无法均匀地分布在多个处理器上，从而影响性能。

● 3. 冗余计算：Key-OIJ算法无法利用在重叠窗口中已处理的数据，导致存在显着的冗余计算。这意味着在处理大窗口时，会进行大量不必要的计算操作，降低了性能。（当窗口大小较大时，匹配时间变得更加占主导地位，因为需要更多时间进行窗口聚合。相反，当窗口大小适中但延迟较大时，查找时间远远超过匹配时间。这是由于无序元组到达更多，Key-OIJ需要为每个间隔连接访问更多的元组。）

新方法—-scale-OIJ

● 整体上，该设计遵循基于键的分区模型（Key-OIJ），但允许根据工作负载分布和相同分区的共享处理来动态重新分区数据。通过精心设计的数据结构和并发模型，提出了一种轻量级的动态调度算法，以实现高度平衡的适应性，而无需数据复制或迁移。

● Time-Travel Data Structure

为了实现高效的窗口数据检索，文章设计了一种基于double-layered skip-list的数据结构。该数据结构的第一层是用于存储<key，second-layer skip-list>，而第二层是用于存储<timestamp,Tuple>。搜索时：首先在第一层 skip-list中搜索以key为关键字的第二层skip-list，然后在第二层 skip-list中搜索以时间戳为关键字的元组（tuple）

时间复杂度：O(logNkey) + O(logNts)（在实验中，随着lateness的增加，吞吐量上新方法优势巨大）

SWMR Concurrency Property：具有相同键的元组可以由多个连接器（joiners）共同处理

● Dynamic Schedule

shared Processin：通过共享处理框架和虚拟团队的设计，连接器可以共享具有相同键的元组，并且可以在不影响正确性的情况下随机分配给virtual team的任何成员进行处理，而不会影响正确性。

Dynamic Schedule：

共享处理框架允许在不迁移数据的情况下动态重新分区数据。通过在运行时收集数据分布统计信息，可以推导出所有连接器的工作负载分布，并基于此定期重新调度分区分配（即键分区调度）。重新调度的目标是减少连接器之间工作负载调度的不平衡性。（ALgorithm3）

● Incremental Online Interval Join

重叠窗口问题：在进行区间连接时，特别是当窗口较大时，存在邻近窗口可能重叠的高概率，这会导致重复的数据访问和计算。

为了解决重叠窗口问题，文章提出了Incremental Online Interval Join。该方法通过使用增量计算和数据结构维护，避免了重复的数据访问和计算。

算法

Algorithm1:Search A Tuple
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: <key, ts>
Output: the node containing the matched tuple
1 node ← HEAD
2 level ← HEIGHT
3 while true do
4 next = load_acquire (node[level].next)
5 if next == NULL || next.key > key then
6 if level <= 0 then
7 return node
8 level = level − 1
9 else if next.key == key then
10 return node
11 else
12 node = next
13 return node

skiplist.h:

使用 FindEqual 方法来寻找 skiplist 中的一个 tuple。这个方法接受一个键值作为参数，然后返回与该键值相等的节点。

这是 FindEqual 方法的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Node<K, V>* FindEqual(const K& key) {
    Node<K, V>* node = head_;
    uint8_t level = GetMaxHeight() - 1;
    while (true) {
        Node<K, V>* next = node->GetNext(level);
        if (next == NULL || compare_(next->GetKey(), key) > 0) {
            if (level <= 0) {
                return node;
            }
            level--;
        } else {
            node = next;
        }
    }
}

你可以这样使用它：

1
2
3
4
5
6
7
8
Skiplist<int, int> skiplist;
// ... 添加一些元素到 skiplist ...
int key = 10;  // 要查找的键值
Node<int, int>* node = skiplist.FindEqual(key);
if (node != NULL) {
    // 找到了节点，可以获取它的值
    int value = node->GetValue();
}

注意，如果 skiplist 中不存在与给定键值相等的节点，FindEqual 方法将返回一个与键值最接近的节点。

Algorithm2: Put A New Tuple
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input: <key, ts, x>
Output: N.A.
// search the position to insert
1 node ← HEAD
2 level ← HEIGHT
3 while true do
4 next = node[level].next
5 if next == NULL || next.key >= key then
6 pre[level] = node
7 if level <= 0 then
8 break
9 level = level − 1
10 else
11 node = next
// insert into the skiplist
12 new_node = NewNode(x, random_height)
13 for i ← 0 to height do
14 store_relaxed(new_node[i].next, pre[i].next)
15 for i ← 0 to height do
16 store_release(pre[i].next, new_node)

skiplist.h:

使用 AddToFirst 方法来向 skiplist 中添加一个新的 tuple。这个方法接受一个键值和一个值作为参数，然后创建一个新的节点并将其添加到 skiplist 的头部。

这是 AddToFirst 方法的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool AddToFirst(const K& key, V& value) {  // NOLINT
    Node<K, V>* node = head_->GetNext(0);
    if (node != NULL && compare_(key, node->GetKey()) > 0) {
        return false;
    }
    uint8_t height = RandomHeight();
    Node<K, V>* pre[MaxHeight];
    for (uint8_t i = 0; i < height; i++) {
        pre[i] = head_;
    }
    if (height > GetMaxHeight()) {
        max_height_.store(height, std::memory_order_relaxed);
    }
    Node<K, V>* node = NewNode(key, value, height);
    if (pre[0]->GetNext(0) == NULL) {
        tail_.store(node, std::memory_order_release);
    }
    for (uint8_t i = 0; i < height; i++) {
        node->SetNextNoBarrier(i, pre[i]->GetNextNoBarrier(i));
        pre[i]->SetNext(i, node);
    }
    return true;
}

你可以这样使用它：

1
2
3
4
5
6
7
8
9
Skiplist<int, int> skiplist;
int key = 10;  // 要添加的键值
int value = 20;  // 要添加的值
bool success = skiplist.AddToFirst(key, value);
if (success) {
    // 添加成功
} else {
    // 添加失败，可能是因为已经存在一个键值大于给定键值的节点
}

注意，如果 skiplist 中已经存在一个键值大于给定键值的节点，AddToFirst 方法将返回 false。

Algorithm3: Dynamic Schedule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Input: Load distribution of all the keys, current key partition
schedule S
Output: optimized key partition schedule
1 Snew = S
2 while true do
3 calculate the workload Wi for every joiner Ji according
to Equation 3
4 select the maximum and minimum joiners:
Jmax = arg maxi Wi
Jmin = arg mini Wi
5 add all key partitions ∀pj ∈ Jmax → priority queue
P QJmax
6 for pi ← P QJmax .top() do
7 replicate pi to Jmin in the new schedule Snew
8 if last_unbalancedness − unbalancedness > δ
then
9 break
10 P QJmax .pop()
11 if Snew does not change then
12 break
13 ∀k |xk| = λ × |xk|
14 return the new schedule Snew

968b9ceba0c63a5cf96ee3ea0e8ae65

Dynamic schedule

Dynamic Schedule算法通过收集运行时的数据分布统计信息，可以推导出所有Joiner的工作负载分布情况，从而可以定期重新调度分区分配（即键分区计划）。

Shared Processing

在这篇文章中，Shared Processing是指一种共享处理框架，用于处理具有相同键的元组。Shared Processing框架允许多个Joiner共同处理具有相同键的元组，从而实现更好的性能和效率。

具体来说，Shared Processing框架使用了一种虚拟团队的概念，将具有相同键的元组分配给多个Joiner共同处理。这些Joiner共同组成一个虚拟团队，共同处理具有相同键的元组。在处理过程中，元组可以随机分配给虚拟团队中的任何一个成员，而不会影响正确性。Joiner向虚拟团队中的所有成员公开读取(R)权限，而将写入(W)权限保留给自己。虚拟团队通过键（特别是键哈希范围）和分区集之间的映射来维护，这个映射在新的调度之后会被原子地替换。每个Joiner被分配的元组都会插入(W)到自己的索引中，而在进行区间连接时，它可以从虚拟团队的所有成员中读取(R)索引。因此，虚拟团队中的每个Joiner都将共享具有相同键的元组的一部分。Shared Processing框架使用了时间旅行索引的SWMR属性来保证正确性和有效性。

通过使用Shared Processing框架，可以实现更好的性能和效率，特别是在处理具有相同键的元组时。Shared Processing框架可以减少重复计算和数据检索，从而提高计算效率和性能表现。

7d94cc65bd6eda404cde47290e67932

Virtual Team

在这篇文章中，Virtual Team是指一组Joiner，它们共同处理具有相同键的元组。Virtual Team是Shared Processing框架的核心概念之一，用于实现多个Joiner共同处理具有相同键的元组，从而提高性能和效率。

具体来说，Virtual Team是由具有相同键的元组随机分配给多个Joiner组成的。这些Joiner共同组成一个虚拟团队，共同处理具有相同键的元组。在处理过程中，元组可以随机分配给虚拟团队中的任何一个成员，而不会影响正确性。Joiner向虚拟团队中的所有成员公开读取(R)权限，而将写入(W)权限保留给自己。虚拟团队通过键（特别是键哈希范围）和分区集之间的映射来维护，这个映射在新的调度之后会被原子地替换。每个Joiner被分配的元组都会插入(W)到自己的索引中，而在进行区间连接时，它可以从虚拟团队的所有成员中读取(R)索引。因此，虚拟团队中的每个Joiner都将共享具有相同键的元组的一部分。

通过使用Virtual Team，可以实现多个Joiner共同处理具有相同键的元组，从而减少重复计算和数据检索，提高计算效率和性能表现。同时，Virtual Team还可以实现更好的负载均衡和资源利用率，从而提高整个系统的性能和效率。

Dynamic schedule

动态调度框架中重新调度的目标是减少Joiner之间工作负载调度的不平衡性。通过在运行时收集数据分布统计信息，我们可以推导出所有Joiner的工作负载分布，并基于此定期重新调度分区分配（即键分区计划）。共享处理框架允许在不进行数据迁移的情况下动态重新分区数据。

重新调度的目标是减少Joiner之间工作负载分布的不平衡性（如公式2所定义）。具体来说，Dynamic Schedule算法将问题形式化为以下两个部分：

ec9316c6792ddbf3adf6f5576d16a9b

a) 问题定义：给定P个分区和J个Joiner，将每个Pi分配给Jj，其中每个Pi可以分配给多个Joiner Jj…Jk。

b) 目标：arg minS unbalancedness，其中S是键分区计划，unbalancedness是工作负载分布的不平衡度量。由于在分区调度期间，我们无法预知未来的元组分布情况，因此我们使用公式3来估计每个Joiner的工作负载（即处理的元组的估计数量）。

30f8251ce7c6b4b55a27993e63183e2

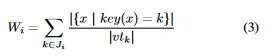
其中，{x | key(x) = k}是所有Joiner处理的具有键k的元组集合，而|vtk|是键k的虚拟团队的大小。对于每个Joiner，我们汇总该Joiner当前处理的所有键的共享工作负载。

1
NP-hard是指一类计算问题，这些问题在多项式时间内无法求解，但是可以在多项式时间内验证其解的正确性。这意味着，如果一个问题是NP-hard，那么它很可能是无法在多项式时间内求解的，需要使用启发式算法或其他近似算法来解决。

为了避免数据迁移开销，我们只允许共享分区的所有权，而不是将其转移到另一个Joiner。因此，基于旧的分区计划的Joiner被保证在基于新的分区计划的键的虚拟团队中。这自然地解决了在调度更改期间分区器和Joiner之间传输缓冲区中元组的正确性问题。

通过使用Dynamic Schedule算法，可以实现更好的负载均衡和性能表现。Dynamic Schedule算法可以动态地调整分区分配，以适应不同的工作负载情况，从而提高计算效率和性能表现。同时，Dynamic Schedule算法还可以实现更好的资源利用率和系统可扩展性，从而提高整个系统的性能和效率。

1
2
3
4
5
6
7
算法3的启发式解决方案的基本步骤是：

1）计算每个Joiner的工作负载，并选择具有最大工作负载Jmax和最小工作负载Jmin的Joiner（第3-4行）。
2）尝试将Jmax中具有最大工作负载的分区复制到Jmin中（第5-7行）。
3）如果不平衡度降低了一个阈值，就退出（第8-9行），并重复步骤1）-2）。
4）如果在迭代后新计划中没有变化，则停止探索（第11-12行）。
5）最后衰减统计数据（第13行）。